Self-gravitational force calculation of infinitely thin gaseous disks
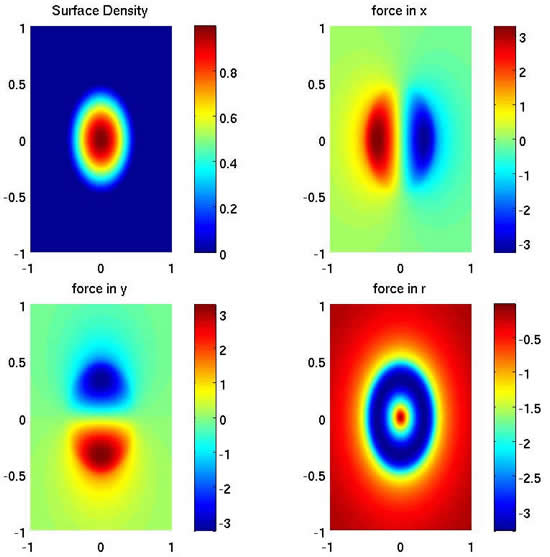
The numerical solutions of a D2 disk for N=1024, the profiles are surface density (left-top), the x-directional force (right-top), the y-directional force(left-bottom), and radial force(right-bottom).
A thin gaseous disk has often been investigated in the context of various phenomena in galaxies, such as, starburst rings, dense circumnuclear molecular disks and the apparent gas hole toward the galactic center. The effect of the self-gravitating force of the gas in the disk may be necessary in confronting observation and numerical simulations in detail. The self-gravitating force calculation can be determined by taking the derivative of the potential which satisfies the Poisson equation. The Poisson equation for such infinitely thin gaseous disks is intrinsically 3-dimensional and its solution can be computationally prohibitive. We propose not to solve the complete potential function problem, but rather simply to calculate the force in infinite planes by the reproducing kernel method. More precisely, representing the force as a double summation of a convolution of the surface density and a fundamental kernel and employing fast Fourier transform, the entire computational complexity can be reduced from O(N2×N2) to O(N2(log2N)2),where N is the number of zones in one dimension. This approach is fast and the periodic boundary condition is not assumed. Therefore, this method is similar to a spectral method, but does not require the imposition of a periodic boundary condition. We further show this approach is of near second order accuracy for smooth surface density. As an application, we investigate the stability of such disks. (C.C. Yen, R.E. Taam, Ken H.C. Yeh, and K.C. Jea, 2012 Submitted)